Cara menghitung nilai rata rata – Pernahkah Anda bertanya-tanya bagaimana menentukan nilai tengah dari sekumpulan angka? Atau bagaimana mengukur kinerja suatu tim berdasarkan data yang ada? Nah, itulah fungsi dari nilai rata-rata! Nilai rata-rata, dalam matematika, adalah representasi tunggal yang menggambarkan nilai tengah dari sekumpulan data. Konsep ini sangat penting dalam berbagai bidang, mulai dari ilmu pengetahuan hingga bisnis, dan bahkan dalam kehidupan sehari-hari.

Dalam artikel ini, kita akan menjelajahi dunia nilai rata-rata, mulai dari pengertian dasar hingga cara menghitungnya, contoh penerapannya, dan bahkan keterbatasannya. Mari kita selami bersama!

Pengertian Nilai Rata-Rata

Nilai rata-rata, atau yang sering disebut dengan mean, merupakan konsep dasar dalam matematika yang digunakan untuk mewakili nilai tengah dari sekumpulan data. Nilai rata-rata membantu kita memahami gambaran umum dari suatu kumpulan data dengan memberikan satu nilai yang mewakili seluruh data tersebut.

Contoh Nilai Rata-Rata dalam Kehidupan Sehari-hari

Misalnya, jika kita ingin mengetahui rata-rata nilai ujian matematika di kelas, kita dapat menjumlahkan semua nilai ujian dan membaginya dengan jumlah siswa di kelas tersebut. Hasilnya akan menjadi nilai rata-rata ujian matematika di kelas tersebut. Contoh lain, ketika kita ingin mengetahui rata-rata tinggi badan siswa di kelas, kita dapat menjumlahkan tinggi badan semua siswa dan membaginya dengan jumlah siswa. Hasilnya akan menjadi rata-rata tinggi badan siswa di kelas tersebut.

Jenis-jenis Rata-Rata

Ada beberapa jenis rata-rata yang digunakan dalam matematika, masing-masing dengan rumus dan contoh penerapan yang berbeda. Berikut adalah beberapa jenis rata-rata yang umum digunakan:

Jenis Rata-Rata	Rumus	Contoh Penerapan
Rata-rata Aritmetika	Jumlah semua data dibagi dengan banyaknya data	Menghitung rata-rata nilai ujian, rata-rata tinggi badan siswa, rata-rata suhu harian
Rata-rata Geometri	Akar pangkat n dari perkalian n buah data	Menghitung pertumbuhan rata-rata investasi, rata-rata pertumbuhan populasi
Rata-rata Harmonis	Jumlah kebalikan dari setiap data dibagi dengan banyaknya data, kemudian dibalik hasilnya	Menghitung kecepatan rata-rata perjalanan, rata-rata resistensi listrik

Rumus Menghitung Nilai Rata-Rata

Menghitung nilai rata-rata adalah hal yang sering kita lakukan dalam kehidupan sehari-hari, baik untuk menganalisis data, mengukur kinerja, atau sekadar mengetahui nilai tengah dari sekumpulan data. Rumus yang digunakan untuk menghitung nilai rata-rata cukup sederhana, namun penting untuk memahami setiap komponennya agar dapat diterapkan dengan benar.

Rumus Umum Menghitung Nilai Rata-Rata

Rumus umum untuk menghitung nilai rata-rata adalah sebagai berikut:

Rata-rata = (Jumlah semua nilai) / (Jumlah data)

Rumus ini menunjukkan bahwa untuk mendapatkan nilai rata-rata, kita perlu menjumlahkan semua nilai data yang kita miliki, kemudian membaginya dengan jumlah total data tersebut.

Penjelasan Variabel dalam Rumus

• Jumlah semua nilai: Merupakan hasil penjumlahan dari semua nilai data yang ingin kita hitung rata-ratanya. Misalnya, jika kita ingin menghitung rata-rata nilai ujian 5 siswa, maka jumlah semua nilai adalah hasil penjumlahan nilai ujian kelima siswa tersebut.
• Jumlah data: Merupakan jumlah total data yang ingin kita hitung rata-ratanya. Dalam contoh sebelumnya, jumlah data adalah 5, karena kita memiliki 5 nilai ujian siswa.

Contoh Penerapan Rumus

Misalnya, kita ingin menghitung nilai rata-rata ujian 5 siswa dengan nilai sebagai berikut:

Siswa	Nilai Ujian
A	80
B	75
C	90
D	85
E	70

Maka, nilai rata-rata ujian kelima siswa tersebut dapat dihitung dengan rumus:

Rata-rata = (80 + 75 + 90 + 85 + 70) / 5 = 400 / 5 = 80

Jadi, nilai rata-rata ujian kelima siswa tersebut adalah 80.

Cara Menghitung Nilai Rata-Rata

Nilai rata-rata, juga dikenal sebagai mean, adalah salah satu ukuran statistik yang paling umum digunakan. Rata-rata memberikan gambaran umum tentang nilai tengah dari sekumpulan data. Rata-rata dapat digunakan untuk berbagai tujuan, seperti menganalisis data, membandingkan data dari kelompok yang berbeda, dan membuat prediksi.

Cara Menghitung Nilai Rata-Rata Secara Manual

Untuk menghitung nilai rata-rata secara manual, kita perlu menjumlahkan semua nilai dalam kumpulan data dan membaginya dengan jumlah total nilai dalam kumpulan data tersebut.

• Langkah 1: Jumlahkan semua nilai dalam kumpulan data.
• Langkah 2: Hitung jumlah total nilai dalam kumpulan data.
• Langkah 3: Bagilah jumlah total nilai dengan jumlah total nilai dalam kumpulan data.

Contoh Perhitungan Nilai Rata-Rata, Cara menghitung nilai rata rata

Misalkan kita memiliki kumpulan data berikut:

Nilai
10
15
20
25
30

Untuk menghitung nilai rata-rata dari kumpulan data ini, kita dapat mengikuti langkah-langkah berikut:

• Langkah 1: Jumlahkan semua nilai dalam kumpulan data: 10 + 15 + 20 + 25 + 30 = 100
• Langkah 2: Hitung jumlah total nilai dalam kumpulan data: 5
• Langkah 3: Bagilah jumlah total nilai dengan jumlah total nilai dalam kumpulan data: 100 / 5 = 20

Jadi, nilai rata-rata dari kumpulan data ini adalah 20.

Rumus Menghitung Nilai Rata-Rata:

Rata-rata = Jumlah semua nilai / Jumlah total nilai

Contoh Penerapan Nilai Rata-Rata: Cara Menghitung Nilai Rata Rata

Nilai rata-rata merupakan alat yang sangat berguna dalam berbagai bidang, baik dalam kehidupan sehari-hari maupun dalam dunia profesional. Dengan menghitung rata-rata, kita dapat memperoleh gambaran umum tentang suatu kumpulan data dan membantu dalam pengambilan keputusan yang lebih tepat.

Rata-rata dalam Dunia Pendidikan

Nilai rata-rata sangat penting dalam dunia pendidikan. Guru menggunakan nilai rata-rata untuk menilai kinerja siswa secara keseluruhan. Misalnya, nilai rata-rata ujian semester digunakan untuk menentukan nilai akhir siswa dalam suatu mata pelajaran. Nilai rata-rata juga digunakan untuk menentukan peringkat siswa dalam kelas, sehingga dapat membantu dalam mengidentifikasi siswa yang berprestasi tinggi dan siswa yang membutuhkan bantuan tambahan.

Rata-rata dalam Bisnis

Dalam bisnis, nilai rata-rata digunakan untuk menganalisis data penjualan, produksi, dan keuangan. Misalnya, perusahaan dapat menghitung rata-rata penjualan bulanan untuk mengetahui tren penjualan dan membuat perencanaan yang lebih efektif. Rata-rata juga digunakan untuk mengukur kinerja karyawan, seperti rata-rata waktu penyelesaian tugas atau rata-rata tingkat kesalahan.

Rata-rata dalam Kesehatan

Nilai rata-rata juga memiliki peran penting dalam bidang kesehatan. Dokter dan perawat menggunakan nilai rata-rata untuk memantau kondisi pasien, seperti suhu tubuh, tekanan darah, dan kadar gula darah. Data rata-rata membantu dalam mengidentifikasi perubahan signifikan dalam kondisi pasien dan menentukan tindakan medis yang tepat.

Rata-rata dalam Ilmu Pengetahuan

Dalam ilmu pengetahuan, nilai rata-rata digunakan untuk menganalisis data eksperimen dan penelitian. Misalnya, dalam penelitian ilmiah, rata-rata digunakan untuk menghitung hasil eksperimen dan menentukan apakah terdapat perbedaan yang signifikan antara kelompok kontrol dan kelompok perlakuan.

Jenis-Jenis Rata-Rata

Rata-rata merupakan nilai yang mewakili seluruh data dalam suatu kumpulan. Namun, tidak semua data dapat direpresentasikan dengan jenis rata-rata yang sama. Terdapat beberapa jenis rata-rata yang umum digunakan, masing-masing memiliki keunggulan dan kekurangan dalam mewakili data.

Rata-Rata Aritmetika

Rata-rata aritmetika merupakan jenis rata-rata yang paling umum digunakan. Jenis ini dihitung dengan menjumlahkan semua nilai data dan kemudian dibagi dengan jumlah total data. Rata-rata aritmetika cocok digunakan untuk data yang terdistribusi normal dan tidak memiliki outlier yang signifikan.

Rumus:

Rata-rata = Σx / n

Keterangan:

Σx = Jumlah semua nilai data

n = Jumlah total data

Contoh: Misalkan terdapat nilai ujian 5 siswa sebagai berikut: 70, 80, 90, 85, dan 95. Maka rata-rata nilai ujian kelima siswa tersebut adalah:

Rata-rata = (70 + 80 + 90 + 85 + 95) / 5 = 420 / 5 = 84

Rata-Rata Geometrik

Rata-rata geometrik digunakan untuk menghitung rata-rata dari data yang menunjukkan pertumbuhan atau perubahan secara eksponensial. Jenis ini cocok untuk data yang memiliki nilai yang sangat bervariasi atau data yang menunjukkan tren pertumbuhan.

Rumus:

Rata-rata Geometrik = (x1 * x2 * … * xn)^(1/n)

Keterangan:

x1, x2, … xn = Nilai data

n = Jumlah total data

Contoh: Misalkan terdapat pertumbuhan penjualan suatu produk selama 3 tahun sebagai berikut: 10%, 15%, dan 20%. Maka rata-rata pertumbuhan penjualan selama 3 tahun tersebut adalah:

Rata-rata Geometrik = (1.10 * 1.15 * 1.20)^(1/3) = 1.148

Artinya, rata-rata pertumbuhan penjualan selama 3 tahun tersebut adalah 14.8% per tahun.

Rata-Rata Harmonik

Rata-rata harmonik digunakan untuk menghitung rata-rata dari data yang memiliki nilai balik atau kebalikan. Jenis ini cocok untuk data yang menunjukkan hubungan timbal balik, seperti kecepatan, waktu, atau konsumsi bahan bakar.

Rumus:

Rata-rata Harmonik = n / (1/x1 + 1/x2 + … + 1/xn)

Keterangan:

x1, x2, … xn = Nilai data

n = Jumlah total data

Contoh: Misalkan terdapat 3 pekerja yang mengerjakan suatu proyek dengan kecepatan masing-masing 10 unit/jam, 15 unit/jam, dan 20 unit/jam. Maka rata-rata kecepatan ketiga pekerja tersebut adalah:

Rata-rata Harmonik = 3 / (1/10 + 1/15 + 1/20) = 3 / (0.1 + 0.067 + 0.05) = 3 / 0.217 = 13.82 unit/jam

Rata-Rata Kuadrat

Rata-rata kuadrat digunakan untuk menghitung rata-rata dari data yang menunjukkan kuadrat nilai data. Jenis ini cocok untuk data yang menunjukkan hubungan kuadrat, seperti luas, volume, atau energi.

Rumus:

Rata-rata Kuadrat = √(Σx^2 / n)

Keterangan:

x1, x2, … xn = Nilai data

n = Jumlah total data

Contoh: Misalkan terdapat 4 buah kotak dengan luas masing-masing 10 cm², 15 cm², 20 cm², dan 25 cm². Maka rata-rata luas keempat kotak tersebut adalah:

Rata-rata Kuadrat = √((10² + 15² + 20² + 25²) / 4) = √(1250 / 4) = √312.5 = 17.68 cm²

Rata-Rata Modus

Rata-rata modus merupakan nilai yang paling sering muncul dalam suatu kumpulan data. Jenis ini cocok untuk data yang memiliki nilai yang berulang dan ingin diketahui nilai yang paling dominan.

Rumus:

Tidak ada rumus khusus untuk menghitung rata-rata modus.

Contoh: Misalkan terdapat data ukuran sepatu 5 orang sebagai berikut: 38, 39, 40, 40, 41. Maka rata-rata modus dari data tersebut adalah 40, karena nilai 40 muncul paling banyak (2 kali) dalam data tersebut.

Pemilihan jenis rata-rata yang tepat sangat penting untuk mendapatkan representasi data yang akurat. Jenis rata-rata yang dipilih harus sesuai dengan jenis data dan tujuan analisis yang ingin dicapai.

Kegunaan Nilai Rata-Rata

Nilai rata-rata merupakan konsep dasar dalam statistika yang memiliki banyak kegunaan dalam berbagai bidang kehidupan. Nilai rata-rata memberikan gambaran umum tentang suatu kumpulan data dan membantu dalam menganalisis dan menginterpretasikan informasi yang terkandung di dalamnya.

Manfaat Penggunaan Nilai Rata-Rata

Penggunaan nilai rata-rata memberikan beberapa manfaat, di antaranya:

• Mempermudah pemahaman data: Nilai rata-rata meringkas kumpulan data yang besar menjadi satu angka tunggal, sehingga lebih mudah dipahami dan diinterpretasikan.
• Membandingkan data: Nilai rata-rata memungkinkan kita untuk membandingkan kumpulan data yang berbeda, baik dalam waktu yang berbeda maupun di tempat yang berbeda.
• Memprediksi tren: Nilai rata-rata dapat digunakan untuk memprediksi tren atau pola dalam data, seperti tren pertumbuhan ekonomi atau perubahan suhu rata-rata.
• Mengidentifikasi outlier: Nilai rata-rata dapat membantu mengidentifikasi data yang tidak biasa atau outlier, yang dapat menunjukkan adanya kesalahan pengukuran atau faktor-faktor khusus yang memengaruhi data.

Analisis Data dengan Nilai Rata-Rata

Nilai rata-rata merupakan alat yang penting dalam analisis data. Dalam analisis data, nilai rata-rata dapat digunakan untuk:

• Menghitung rata-rata sampel: Nilai rata-rata sampel digunakan untuk memperkirakan rata-rata populasi.
• Menganalisis data kelompok: Nilai rata-rata dapat digunakan untuk membandingkan data dari kelompok yang berbeda, seperti nilai rata-rata ujian siswa di kelas A dan kelas B.
• Menentukan tren dan pola: Nilai rata-rata dapat digunakan untuk mengidentifikasi tren dan pola dalam data, seperti tren pertumbuhan penjualan atau perubahan suhu rata-rata.
• Membuat prediksi: Nilai rata-rata dapat digunakan untuk membuat prediksi tentang data di masa depan, seperti memprediksi penjualan produk di masa depan berdasarkan data penjualan di masa lalu.

Contoh Penggunaan Nilai Rata-Rata

Berikut beberapa contoh penggunaan nilai rata-rata dalam berbagai bidang:

Pendidikan

Dalam bidang pendidikan, nilai rata-rata digunakan untuk:

• Menghitung nilai akhir siswa: Nilai rata-rata digunakan untuk menghitung nilai akhir siswa dari beberapa mata pelajaran.
• Membandingkan prestasi siswa: Nilai rata-rata dapat digunakan untuk membandingkan prestasi siswa dalam kelas yang berbeda atau di sekolah yang berbeda.
• Menilai efektivitas program pembelajaran: Nilai rata-rata dapat digunakan untuk menilai efektivitas program pembelajaran dengan membandingkan nilai rata-rata siswa sebelum dan sesudah program.

Ekonomi

Dalam bidang ekonomi, nilai rata-rata digunakan untuk:

• Menghitung pertumbuhan ekonomi: Nilai rata-rata digunakan untuk menghitung pertumbuhan ekonomi suatu negara.
• Menilai tingkat inflasi: Nilai rata-rata digunakan untuk menilai tingkat inflasi suatu negara.
• Menganalisis data pasar: Nilai rata-rata digunakan untuk menganalisis data pasar, seperti harga rata-rata saham atau harga rata-rata barang.

Bidang Lainnya

Selain pendidikan dan ekonomi, nilai rata-rata juga digunakan dalam berbagai bidang lainnya, seperti:

• Kesehatan: Nilai rata-rata digunakan untuk menghitung tekanan darah rata-rata, suhu tubuh rata-rata, dan sebagainya.
• Ilmu pengetahuan: Nilai rata-rata digunakan untuk menganalisis data penelitian, seperti data hasil eksperimen.
• Teknik: Nilai rata-rata digunakan untuk menghitung nilai rata-rata tegangan, arus, dan sebagainya dalam sistem kelistrikan.

Perbedaan Nilai Rata-Rata dengan Ukuran Statistik Lainnya

Nilai rata-rata, median, dan modus merupakan tiga ukuran statistik yang umum digunakan untuk menggambarkan data. Ketiganya memberikan gambaran yang berbeda tentang pusat data, sehingga penting untuk memahami perbedaannya dan kapan harus menggunakan masing-masing ukuran.

Perbedaan Nilai Rata-Rata, Median, dan Modus

Berikut penjelasan perbedaan nilai rata-rata, median, dan modus:

• Nilai rata-rata adalah jumlah semua nilai dalam kumpulan data dibagi dengan jumlah nilai. Nilai rata-rata sensitif terhadap nilai ekstrem, yang dapat memengaruhi hasil akhir.
• Median adalah nilai tengah dalam kumpulan data yang telah diurutkan dari yang terkecil hingga yang terbesar. Median tidak dipengaruhi oleh nilai ekstrem, sehingga memberikan gambaran yang lebih akurat tentang pusat data ketika terdapat nilai ekstrem.
• Modus adalah nilai yang paling sering muncul dalam kumpulan data. Modus berguna untuk melihat nilai yang paling umum atau populer dalam kumpulan data.

Contoh Data

Misalnya, perhatikan data berikut: 2, 4, 5, 6, 8, 10, 100.

• Nilai rata-rata: (2 + 4 + 5 + 6 + 8 + 10 + 100) / 7 = 20,86
• Median: 6 (nilai tengah setelah data diurutkan)
• Modus: 10 (nilai yang paling sering muncul)

Dalam contoh ini, nilai rata-rata dipengaruhi oleh nilai ekstrem (100), sehingga memberikan gambaran yang tidak akurat tentang pusat data. Median memberikan gambaran yang lebih akurat tentang pusat data, sedangkan modus menunjukkan nilai yang paling umum dalam data.

Tabel Perbandingan

Jenis Ukuran	Rumus	Penerapan
Nilai Rata-Rata	Jumlah semua nilai / Jumlah nilai	Digunakan untuk menggambarkan pusat data ketika tidak terdapat nilai ekstrem.
Median	Nilai tengah dalam kumpulan data yang telah diurutkan	Digunakan untuk menggambarkan pusat data ketika terdapat nilai ekstrem.
Modus	Nilai yang paling sering muncul	Digunakan untuk melihat nilai yang paling umum atau populer dalam kumpulan data.

Keterbatasan Nilai Rata-Rata

Nilai rata-rata, meskipun merupakan alat statistik yang umum digunakan, memiliki keterbatasan yang perlu dipahami. Dalam beberapa kasus, nilai rata-rata mungkin tidak sepenuhnya mewakili data dan dapat memberikan gambaran yang menyesatkan. Penting untuk memahami batasan ini agar kita dapat menginterpretasikan data secara akurat dan membuat keputusan yang tepat.

Pengaruh Outlier

Salah satu keterbatasan utama dari nilai rata-rata adalah sensitivitasnya terhadap outlier, yaitu nilai ekstrem yang berbeda jauh dari data lainnya. Outlier dapat dengan mudah “menarik” nilai rata-rata ke arahnya, sehingga nilai rata-rata tidak lagi menjadi representasi yang akurat dari data keseluruhan.

• Misalnya, perhatikan gaji karyawan di sebuah perusahaan. Jika seorang karyawan memiliki gaji yang sangat tinggi, nilai rata-rata gaji karyawan akan terpengaruh oleh outlier ini. Nilai rata-rata mungkin tampak tinggi, tetapi tidak mencerminkan gaji rata-rata sebagian besar karyawan.

Contoh Keterbatasan

Berikut adalah contoh data yang menunjukkan keterbatasan nilai rata-rata:

Data	Nilai
Gaji Karyawan 1	Rp 5.000.000
Gaji Karyawan 2	Rp 4.500.000
Gaji Karyawan 3	Rp 4.000.000
Gaji Karyawan 4	Rp 3.500.000
Gaji Karyawan 5	Rp 100.000.000

Nilai rata-rata gaji karyawan dalam contoh ini adalah Rp 25.400.000. Namun, nilai ini tidak mencerminkan gaji rata-rata sebagian besar karyawan. Hanya satu karyawan dengan gaji yang sangat tinggi yang “menarik” nilai rata-rata ke atas.

Keterbatasan Lainnya

Selain outlier, nilai rata-rata juga memiliki keterbatasan lain, seperti:

• Tidak mempertimbangkan distribusi data. Nilai rata-rata tidak memberikan informasi tentang bagaimana data tersebar. Data dapat terdistribusi secara merata atau memiliki kecenderungan tertentu, dan nilai rata-rata tidak dapat menangkap informasi ini.
• Tidak dapat digunakan untuk data kategorikal. Nilai rata-rata hanya dapat dihitung untuk data numerik. Data kategorikal, seperti warna atau jenis kelamin, tidak dapat dirata-ratakan.

Teknik Menghitung Nilai Rata-Rata dengan Spreadsheet

Menghitung nilai rata-rata menggunakan spreadsheet merupakan cara yang praktis dan efisien. Spreadsheet seperti Microsoft Excel atau Google Sheets menyediakan fungsi khusus untuk menghitung rata-rata, yang memudahkan kita dalam menganalisis data numerik.

Cara Menghitung Nilai Rata-Rata dengan Spreadsheet

Untuk menghitung nilai rata-rata menggunakan spreadsheet, kita dapat memanfaatkan fungsi “AVERAGE” atau “RATA-RATA” (tergantung pada bahasa spreadsheet yang digunakan). Berikut langkah-langkahnya:

1. Masukkan data numerik yang ingin dihitung rata-ratanya ke dalam sel spreadsheet.
2. Pilih sel kosong untuk menampilkan hasil rata-rata.
3. Ketik rumus “AVERAGE” atau “RATA-RATA” diikuti tanda kurung buka “(“.
4. Pilih sel yang berisi data numerik yang ingin dihitung rata-ratanya. Anda dapat memilih sel secara individual atau memilih rentang sel.
5. Tutup tanda kurung dengan tanda kurung tutup “)” dan tekan tombol “Enter” pada keyboard.

Spreadsheet akan otomatis menghitung dan menampilkan nilai rata-rata dari data yang dipilih.

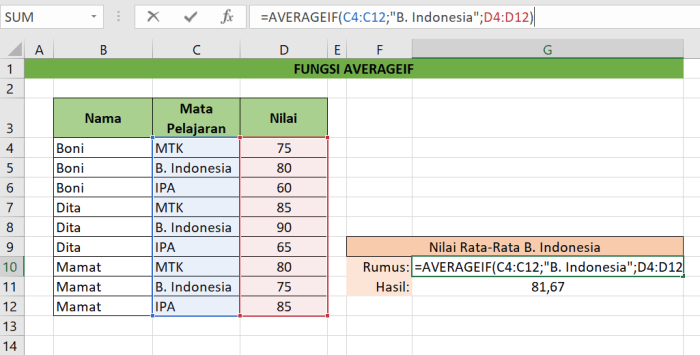
Contoh Penggunaan Formula Rata-Rata pada Spreadsheet

Misalnya, kita memiliki data nilai ujian lima siswa sebagai berikut:

Nama Siswa	Nilai Ujian
Andi	80
Budi	75
Citra	85
Dedi	90
Eka	70

Untuk menghitung nilai rata-rata ujian, kita dapat menggunakan rumus “AVERAGE” atau “RATA-RATA”. Berikut langkah-langkahnya:

1. Pilih sel kosong untuk menampilkan hasil rata-rata.
2. Ketik rumus “AVERAGE(B2:B6)” atau “RATA-RATA(B2:B6)” dan tekan tombol “Enter”.

Spreadsheet akan menampilkan nilai rata-rata ujian yaitu 80.

Ilustrasi Perhitungan Nilai Rata-Rata dengan Spreadsheet

Berikut ilustrasi langkah-langkah perhitungan nilai rata-rata dengan spreadsheet:

1. Masukkan data nilai ujian lima siswa ke dalam sel spreadsheet.
2. Pilih sel kosong untuk menampilkan hasil rata-rata.
3. Ketik rumus “AVERAGE(B2:B6)” atau “RATA-RATA(B2:B6)” dan tekan tombol “Enter”.

Spreadsheet akan menampilkan nilai rata-rata ujian yaitu 80.

Ilustrasi ini menunjukkan bagaimana mudahnya menghitung nilai rata-rata dengan spreadsheet. Fungsi “AVERAGE” atau “RATA-RATA” membantu kita untuk mendapatkan hasil yang akurat dan efisien.

Aplikasi Menghitung Nilai Rata-Rata

Dalam era digital saat ini, menghitung nilai rata-rata tidak lagi menjadi tugas yang rumit. Berbagai aplikasi dan software tersedia untuk membantu kita dengan mudah dan cepat mendapatkan hasil yang akurat. Aplikasi-aplikasi ini menawarkan beragam fitur dan kemudahan akses yang memudahkan pengolahan data, baik untuk keperluan akademis, bisnis, maupun personal.

Aplikasi untuk Menghitung Nilai Rata-rata

Berikut adalah beberapa aplikasi yang dapat digunakan untuk menghitung nilai rata-rata, dilengkapi dengan fitur-fitur unggulan dan contoh penggunaannya:

• Microsoft Excel: Aplikasi spreadsheet yang populer ini memiliki fitur “AVERAGE” untuk menghitung rata-rata dari serangkaian data. Fitur ini sangat mudah digunakan. Anda hanya perlu memilih sel yang berisi data yang ingin dihitung rata-ratanya, kemudian ketik “=AVERAGE(sel1:seln)” dan tekan enter. Contohnya, jika Anda ingin menghitung rata-rata dari nilai di sel A1 hingga A5, maka rumusnya adalah “=AVERAGE(A1:A5)”.
• Google Sheets: Mirip dengan Microsoft Excel, Google Sheets juga memiliki fitur “AVERAGE” yang dapat digunakan untuk menghitung nilai rata-rata. Selain itu, Google Sheets dapat diakses secara online dan memungkinkan kolaborasi dengan pengguna lain.
• Calculator: Aplikasi kalkulator bawaan di smartphone atau komputer umumnya dilengkapi dengan fungsi untuk menghitung rata-rata. Anda hanya perlu memasukkan data yang ingin dihitung rata-ratanya, lalu tekan tombol “rata-rata” atau “mean”.
• Python: Bahasa pemrograman Python memiliki library yang kuat untuk analisis data, termasuk fungsi “mean” yang dapat digunakan untuk menghitung nilai rata-rata dari data yang tersimpan dalam variabel atau array.
• R: Bahasa pemrograman R juga memiliki fungsi “mean” yang dapat digunakan untuk menghitung nilai rata-rata dari data yang tersimpan dalam variabel atau vektor. R sangat populer di kalangan data scientist dan statistikawan.

Simpulan Akhir

Memahami cara menghitung nilai rata-rata adalah langkah awal dalam memahami data dan mengambil keputusan yang lebih baik. Dengan mengetahui berbagai jenis rata-rata, keterbatasannya, dan teknik perhitungan yang efisien, Anda dapat memanfaatkan alat statistik ini untuk analisis data yang lebih akurat dan efektif. Selamat bereksplorasi dan jangan ragu untuk menerapkan pengetahuan baru ini dalam berbagai bidang kehidupan Anda!