Cara Menghitung Determinan Matriks
Daftar Isi
Determinan matriks, sebuah konsep fundamental dalam aljabar linear, memiliki peran penting dalam berbagai bidang, mulai dari menyelesaikan sistem persamaan linear hingga menghitung luas dan volume dalam geometri. Determinan matriks, yang secara sederhana merupakan nilai tunggal yang dihitung dari matriks persegi, menyimpan informasi penting tentang matriks tersebut. Bagaimana cara menghitung determinan matriks? Mari kita telusuri langkah demi langkah, mulai dari matriks sederhana hingga matriks berordo tinggi.
Artikel ini akan membahas secara detail cara menghitung determinan matriks dengan berbagai metode, mulai dari matriks 2×2 yang sederhana hingga matriks berordo tinggi. Anda akan mempelajari metode Sarrus untuk matriks 3×3 dan metode ekspansi kofaktor untuk matriks berordo tinggi. Selain itu, kita akan mengulas sifat-sifat penting determinan dan hubungannya dengan invers matriks, serta bagaimana determinan dapat diaplikasikan dalam berbagai bidang seperti geometri dan fisika.
Pengertian Determinan Matriks
Determinan matriks adalah sebuah nilai skalar yang dihitung dari elemen-elemen dalam matriks persegi. Nilai ini sangat penting dalam aljabar linear, karena memiliki banyak aplikasi dalam berbagai bidang, seperti menyelesaikan sistem persamaan linear, mencari invers matriks, dan menghitung volume bangun ruang. Bayangkan determinan sebagai sebuah angka yang merepresentasikan “kekuatan” atau “keunikan” dari matriks.
Menentukan Determinan Matriks
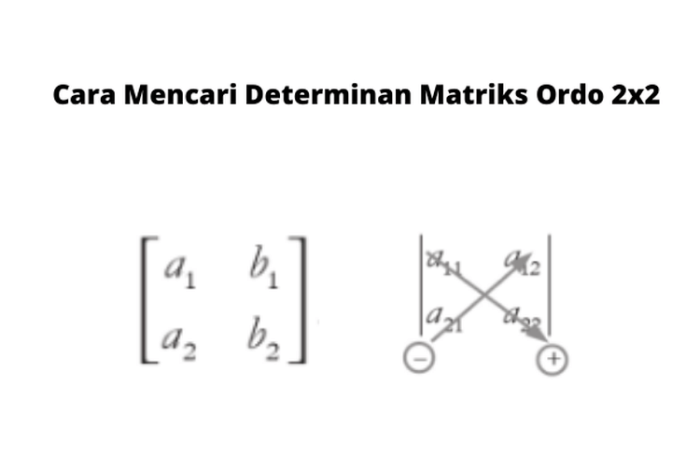
Determinan matriks dapat dihitung dengan beberapa metode, tergantung pada ukuran matriks. Untuk matriks 2×2, determinan dihitung dengan rumus sederhana. Berikut contohnya:
Misalnya, kita memiliki matriks A:
A =
[ 2 3 ]
[ 1 4 ]
Determinan dari matriks A (ditulis sebagai det(A) atau |A|) dihitung sebagai berikut:
det(A) = (2 * 4) – (3 * 1) = 8 – 3 = 5
Untuk matriks berukuran lebih besar, kita dapat menggunakan metode ekspansi kofaktor, yang melibatkan penguraian matriks menjadi sub-matriks yang lebih kecil. Metode ini lebih kompleks, tetapi dapat diterapkan pada matriks dengan ukuran apa pun.
Sifat-sifat Determinan Matriks
Determinan matriks memiliki beberapa sifat penting yang perlu dipahami. Sifat-sifat ini membantu kita dalam menghitung dan menganalisis determinan dengan lebih mudah.
- Determinan matriks identitas adalah 1.
- Determinan matriks nol adalah 0.
- Determinan matriks transpose sama dengan determinan matriks aslinya.
- Determinan hasil perkalian dua matriks sama dengan perkalian determinan kedua matriks tersebut.
- Jika dua baris atau kolom dalam matriks ditukar, determinan akan berubah tanda.
- Jika semua elemen dalam satu baris atau kolom dikalikan dengan konstanta k, determinan akan dikalikan dengan k.
- Determinan matriks singular (matriks yang tidak memiliki invers) adalah 0.
Cara Menghitung Determinan Matriks 3×3
Determinan matriks adalah sebuah nilai skalar yang dapat dihitung dari matriks persegi. Determinan matriks memiliki banyak aplikasi dalam aljabar linear, seperti dalam menyelesaikan sistem persamaan linear, mencari invers matriks, dan menghitung volume suatu bangun ruang.
Pada artikel ini, kita akan membahas cara menghitung determinan matriks 3×3 dengan menggunakan metode Sarrus. Metode Sarrus adalah salah satu metode yang paling mudah dan praktis untuk menghitung determinan matriks 3×3.
Metode Sarrus
Metode Sarrus merupakan metode yang mudah dipahami dan diterapkan untuk menghitung determinan matriks 3×3. Metode ini menggunakan pola khusus untuk mengalikan elemen-elemen matriks dan kemudian menjumlahkan hasil perkalian tersebut.
Berikut langkah-langkah menghitung determinan matriks 3×3 dengan menggunakan metode Sarrus:
- Tuliskan matriks 3×3 yang ingin Anda hitung determinannya.
- Salin dua kolom pertama matriks ke sebelah kanan matriks tersebut.
- Kalikan elemen-elemen pada diagonal utama dan kedua diagonal yang sejajar dengan diagonal utama.
- Kalikan elemen-elemen pada diagonal sekunder dan kedua diagonal yang sejajar dengan diagonal sekunder.
- Jumlahkan hasil perkalian pada langkah 3 dan kurangi dengan jumlah hasil perkalian pada langkah 4.
Berikut contoh matriks 3×3 dan perhitungan determinannya dengan menggunakan metode Sarrus:
Misalkan matriks 3×3 adalah:
A =
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |Langkah-langkah menghitung determinan matriks A dengan metode Sarrus:
1. Tuliskan matriks A dan salin dua kolom pertama ke sebelah kanan matriks:
| 1 2 3 | 1 2 |
| 4 5 6 | 4 5 |
| 7 8 9 | 7 8 |2. Kalikan elemen-elemen pada diagonal utama dan kedua diagonal yang sejajar dengan diagonal utama:
(1 * 5 * 9) + (2 * 6 * 7) + (3 * 4 * 8) = 45 + 84 + 96 = 2253. Kalikan elemen-elemen pada diagonal sekunder dan kedua diagonal yang sejajar dengan diagonal sekunder:
(3 * 5 * 7) + (1 * 6 * 8) + (2 * 4 * 9) = 105 + 48 + 72 = 2254. Jumlahkan hasil perkalian pada langkah 2 dan kurangi dengan jumlah hasil perkalian pada langkah 3:
225 – 225 = 0Jadi, determinan matriks A adalah 0.
Tabel Langkah-Langkah Menghitung Determinan Matriks 3×3 dengan Metode Sarrus
| Langkah | Penjelasan |
|---|---|
| 1 | Tuliskan matriks 3×3 yang ingin Anda hitung determinannya. |
| 2 | Salin dua kolom pertama matriks ke sebelah kanan matriks tersebut. |
| 3 | Kalikan elemen-elemen pada diagonal utama dan kedua diagonal yang sejajar dengan diagonal utama. |
| 4 | Kalikan elemen-elemen pada diagonal sekunder dan kedua diagonal yang sejajar dengan diagonal sekunder. |
| 5 | Jumlahkan hasil perkalian pada langkah 3 dan kurangi dengan jumlah hasil perkalian pada langkah 4. |
Penerapan Determinan Matriks
Determinan matriks, meskipun mungkin tampak seperti konsep abstrak dalam aljabar linear, memiliki aplikasi yang luas dan penting dalam berbagai bidang. Determinan matriks bukan hanya alat matematis, tetapi juga merupakan kunci untuk memahami dan menyelesaikan berbagai masalah dalam ilmu pengetahuan dan teknik.
Penerapan Determinan Matriks dalam Aljabar Linear
Dalam aljabar linear, determinan matriks memainkan peran penting dalam menyelesaikan sistem persamaan linear. Determinan matriks digunakan untuk menentukan apakah sistem persamaan linear memiliki solusi unik, solusi tak hingga, atau tidak memiliki solusi. Determinan matriks juga digunakan untuk menemukan invers matriks, yang penting dalam menyelesaikan sistem persamaan linear dengan metode eliminasi Gauss-Jordan.
Penerapan Determinan Matriks dalam Geometri
Determinan matriks memiliki aplikasi penting dalam geometri, terutama dalam menentukan luas dan volume bangun geometri. Determinan matriks dapat digunakan untuk menghitung luas segitiga dan volume tetrahedron.
- Determinan matriks 2×2 dapat digunakan untuk menghitung luas segitiga yang dibentuk oleh dua vektor. Misalkan kita memiliki dua vektor, a = (a1, a2) dan b = (b1, b2), maka luas segitiga yang dibentuk oleh kedua vektor tersebut adalah setengah dari nilai absolut determinan matriks yang dibentuk oleh kedua vektor tersebut:
Luas Segitiga = 1/2 |det(a, b)| = 1/2 |a1b2 – a2b1|
- Determinan matriks 3×3 dapat digunakan untuk menghitung volume tetrahedron yang dibentuk oleh tiga vektor. Misalkan kita memiliki tiga vektor, a = (a1, a2, a3), b = (b1, b2, b3), dan c = (c1, c2, c3), maka volume tetrahedron yang dibentuk oleh ketiga vektor tersebut adalah sepertiga dari nilai absolut determinan matriks yang dibentuk oleh ketiga vektor tersebut:
Volume Tetrahedron = 1/6 |det(a, b, c)|
Penerapan Determinan Matriks dalam Fisika, Cara menghitung determinan matriks
Determinan matriks juga memiliki aplikasi dalam fisika, terutama dalam mekanika dan elektromagnetisme. Determinan matriks digunakan untuk menghitung momen inersia suatu benda tegar, yang merupakan ukuran resistensi benda terhadap perubahan rotasi. Determinan matriks juga digunakan untuk menghitung medan magnet yang dihasilkan oleh arus listrik, dan untuk menganalisis gelombang elektromagnetik.
Contoh Penerapan Determinan Matriks dalam Menyelesaikan Sistem Persamaan Linear
Misalkan kita memiliki sistem persamaan linear berikut:
2x + 3y = 7
x – y = 1
Sistem persamaan linear ini dapat ditulis dalam bentuk matriks sebagai berikut:
[2 3] [x] = [7]
[1 -1] [y] = [1]
Determinan matriks koefisien adalah:
det([2 3], [1 -1]) = (2)(-1) – (3)(1) = -5
Karena determinan matriks koefisien tidak sama dengan nol, maka sistem persamaan linear ini memiliki solusi unik. Solusi unik untuk sistem persamaan linear ini dapat ditemukan dengan menggunakan metode eliminasi Gauss-Jordan atau dengan menggunakan invers matriks koefisien.
Sifat-sifat Determinan Matriks

Determinan matriks memiliki beberapa sifat penting yang memudahkan manipulasi dan perhitungannya. Sifat-sifat ini membantu kita memahami hubungan antara determinan dan operasi matriks, serta memudahkan dalam menyelesaikan masalah terkait matriks.
Sifat Komutatif
Sifat komutatif menyatakan bahwa determinan matriks tidak bergantung pada urutan baris atau kolomnya. Artinya, menukar dua baris atau dua kolom pada matriks tidak akan mengubah nilai determinannya, hanya akan mengubah tanda determinan.
|A| = |-A|
Sebagai contoh, perhatikan matriks berikut:
A = [[1, 2], [3, 4]]
Determinan A adalah:
|A| = (1 * 4) – (2 * 3) = -2
Jika kita menukar baris pertama dan kedua:
B = [[3, 4], [1, 2]]
Determinan B adalah:
|B| = (3 * 2) – (4 * 1) = 2
Terlihat bahwa |B| = -|A|, yang menunjukkan bahwa determinan matriks tidak bergantung pada urutan baris atau kolomnya.
Sifat Distributif
Sifat distributif menyatakan bahwa determinan dari perkalian skalar dengan matriks sama dengan perkalian skalar tersebut dengan determinan matriks.
|kA| = k|A|
Sebagai contoh, perhatikan matriks A dan skalar k = 2:
A = [[1, 2], [3, 4]]
kA = 2 * [[1, 2], [3, 4]] = [[2, 4], [6, 8]]
Determinan A adalah:
|A| = (1 * 4) – (2 * 3) = -2
Determinan kA adalah:
|kA| = (2 * 8) – (4 * 6) = -4
Terlihat bahwa |kA| = 2 * |A|, yang menunjukkan bahwa determinan dari perkalian skalar dengan matriks sama dengan perkalian skalar tersebut dengan determinan matriks.
Sifat Asosiatif
Sifat asosiatif menyatakan bahwa determinan dari perkalian dua matriks sama dengan perkalian determinan kedua matriks tersebut.
|AB| = |A||B|
Sebagai contoh, perhatikan matriks A dan B:
A = [[1, 2], [3, 4]]
B = [[5, 6], [7, 8]]
Determinan A adalah:
|A| = (1 * 4) – (2 * 3) = -2
Determinan B adalah:
|B| = (5 * 8) – (6 * 7) = -2
Perkalian matriks A dan B adalah:
AB = [[19, 22], [43, 50]]
Determinan AB adalah:
|AB| = (19 * 50) – (22 * 43) = 4
Terlihat bahwa |AB| = |A||B|, yang menunjukkan bahwa determinan dari perkalian dua matriks sama dengan perkalian determinan kedua matriks tersebut.
Tabel Sifat-sifat Determinan Matriks
| Sifat | Rumus | Keterangan |
|---|---|---|
| Komutatif | |A| = |-A| | Determinan matriks tidak bergantung pada urutan baris atau kolomnya. |
| Distributif | |kA| = k|A| | Determinan dari perkalian skalar dengan matriks sama dengan perkalian skalar tersebut dengan determinan matriks. |
| Asosiatif | |AB| = |A||B| | Determinan dari perkalian dua matriks sama dengan perkalian determinan kedua matriks tersebut. |
Penggunaan Determinan Matriks dalam Sistem Persamaan Linear
Determinan matriks tidak hanya bermanfaat dalam aljabar linear, tetapi juga memiliki aplikasi praktis dalam menyelesaikan sistem persamaan linear. Dengan menggunakan determinan, kita dapat menemukan solusi unik untuk sistem persamaan linear dengan jumlah variabel yang sama dengan jumlah persamaan. Metode ini, yang dikenal sebagai aturan Cramer, memberikan pendekatan sistematis untuk menemukan solusi.
Metode Cramer
Metode Cramer memanfaatkan determinan untuk menyelesaikan sistem persamaan linear. Metode ini melibatkan langkah-langkah berikut:
- Tulis sistem persamaan linear dalam bentuk matriks.
- Hitung determinan matriks koefisien, yang dilambangkan dengan D.
- Untuk setiap variabel, ganti kolom matriks koefisien dengan kolom konstanta dan hitung determinan matriks baru ini. Determinan ini dilambangkan dengan Dx, Dy, Dz, dan seterusnya, sesuai dengan variabel yang diganti.
- Solusi untuk setiap variabel diperoleh dengan membagi determinan yang terkait dengan variabel tersebut (Dx, Dy, Dz, dll.) dengan determinan matriks koefisien (D).
Contoh Penggunaan Metode Cramer
Misalkan kita memiliki sistem persamaan linear berikut:
2x + 3y = 7
x – 2y = -1
Untuk menyelesaikan sistem ini dengan metode Cramer, kita ikuti langkah-langkah di atas:
- Matriks koefisien adalah:
- Determinan matriks koefisien (D) adalah:
- Untuk menemukan nilai x, kita ganti kolom pertama matriks koefisien dengan kolom konstanta:
- Untuk menemukan nilai y, kita ganti kolom kedua matriks koefisien dengan kolom konstanta:
- Solusi untuk x dan y adalah:
2 3 1 -2
D = (2)(-2) – (3)(1) = -7
7 3 -1 -2
Determinan matriks ini (Dx) adalah:
Dx = (7)(-2) – (3)(-1) = -11
2 7 1 -1
Determinan matriks ini (Dy) adalah:
Dy = (2)(-1) – (7)(1) = -9
x = Dx / D = -11 / -7 = 11/7
y = Dy / D = -9 / -7 = 9/7
Oleh karena itu, solusi unik untuk sistem persamaan linear ini adalah x = 11/7 dan y = 9/7.
Aplikasi Determinan Matriks dalam Geometri
Determinan matriks memiliki aplikasi yang luas dalam geometri, terutama dalam menghitung luas, volume, dan menentukan posisi relatif titik terhadap garis dan bidang. Dengan memahami hubungan antara determinan dan geometri, kita dapat menyelesaikan berbagai masalah geometri dengan mudah dan efisien.
Menghitung Luas Segitiga
Determinan matriks dapat digunakan untuk menghitung luas segitiga yang dibentuk oleh tiga titik di bidang Cartesian. Jika tiga titik tersebut adalah (x1, y1), (x2, y2), dan (x3, y3), maka luas segitiga dapat dihitung dengan rumus:
Luas segitiga = 1/2 * |det(A)|
di mana A adalah matriks:
A =
| 1 x1 y1 |
| 1 x2 y2 |
| 1 x3 y3 |
Misalnya, perhatikan segitiga dengan titik-titik (1, 2), (3, 4), dan (5, 1). Matriks A yang sesuai adalah:
A =
| 1 1 2 |
| 1 3 4 |
| 1 5 1 |
Determinan dari A adalah -12, sehingga luas segitiga adalah 1/2 * |-12| = 6 satuan persegi.
Menghitung Volume Tetrahedron
Determinan matriks juga dapat digunakan untuk menghitung volume tetrahedron yang dibentuk oleh empat titik dalam ruang tiga dimensi. Jika keempat titik tersebut adalah (x1, y1, z1), (x2, y2, z2), (x3, y3, z3), dan (x4, y4, z4), maka volume tetrahedron dapat dihitung dengan rumus:
Volume tetrahedron = 1/6 * |det(B)|
di mana B adalah matriks:
B =
| 1 x1 y1 z1 |
| 1 x2 y2 z2 |
| 1 x3 y3 z3 |
| 1 x4 y4 z4 |
Sebagai contoh, perhatikan tetrahedron dengan titik-titik (1, 0, 0), (0, 1, 0), (0, 0, 1), dan (1, 1, 1). Matriks B yang sesuai adalah:
B =
| 1 1 0 0 |
| 1 0 1 0 |
| 1 0 0 1 |
| 1 1 1 1 |
Determinan dari B adalah 2, sehingga volume tetrahedron adalah 1/6 * |2| = 1/3 satuan kubik.
Menentukan Posisi Titik Relatif terhadap Garis dan Bidang
Determinan matriks juga dapat digunakan untuk menentukan posisi titik relatif terhadap garis dan bidang. Misalnya, untuk menentukan apakah suatu titik terletak pada garis, kita dapat membentuk matriks yang terdiri dari koordinat titik dan dua titik pada garis. Jika determinan matriks ini sama dengan nol, maka titik tersebut terletak pada garis.
Demikian pula, untuk menentukan apakah suatu titik terletak pada bidang, kita dapat membentuk matriks yang terdiri dari koordinat titik dan tiga titik pada bidang. Jika determinan matriks ini sama dengan nol, maka titik tersebut terletak pada bidang.
Determinan Matriks dalam Fisika
Determinan matriks merupakan konsep matematika yang memiliki aplikasi penting dalam berbagai bidang ilmu pengetahuan, termasuk fisika. Dalam konteks fisika, determinan matriks dapat digunakan untuk menyelesaikan persamaan diferensial, menganalisis sistem fisika, dan bahkan dalam teori kuantum. Dalam pembahasan ini, kita akan menjelajahi bagaimana determinan matriks berperan penting dalam beberapa aspek fisika, seperti mekanika kuantum dan teori medan.
Mekanika Kuantum
Dalam mekanika kuantum, determinan matriks berperan penting dalam menyelesaikan persamaan Schrödinger, persamaan yang mendeskripsikan perilaku partikel pada tingkat atom. Persamaan Schrödinger merupakan persamaan diferensial yang melibatkan operator kuantum, yang dapat direpresentasikan dalam bentuk matriks. Untuk mencari solusi persamaan Schrödinger, kita perlu mencari nilai eigen dari operator kuantum, yang dapat dilakukan dengan mencari determinan dari matriks operator kuantum.
- Determinan matriks operator kuantum memberikan informasi tentang energi partikel, yang merupakan nilai eigen dari operator energi.
- Determinan matriks juga digunakan untuk menentukan kemungkinan menemukan partikel dalam keadaan tertentu, yang diwakili oleh vektor eigen dari operator kuantum.
Teori Medan
Teori medan, yang membahas interaksi antara partikel fundamental, juga memanfaatkan determinan matriks dalam berbagai cara. Salah satu contohnya adalah dalam teori medan kuantum, di mana determinan matriks digunakan untuk menghitung amplitudo probabilitas untuk proses tertentu. Amplitudo probabilitas merupakan besaran kompleks yang menentukan kemungkinan terjadinya suatu proses dalam teori medan kuantum.
- Determinan matriks juga digunakan untuk menghitung propagator partikel, yang menggambarkan bagaimana partikel menyebar dalam ruang dan waktu.
- Dalam teori medan gauge, determinan matriks digunakan untuk menentukan potensial interaksi antara partikel, yang merupakan faktor penting dalam memahami sifat-sifat gaya fundamental.
Contoh Penggunaan Determinan Matriks dalam Fisika
Sebagai contoh, perhatikan kasus partikel yang bergerak dalam medan potensial. Energi partikel dapat dihitung dengan mencari nilai eigen dari operator energi, yang direpresentasikan sebagai matriks. Determinan dari matriks operator energi memberikan informasi tentang energi partikel. Dengan kata lain, determinan matriks dapat digunakan untuk menentukan energi partikel dalam sistem kuantum.
Energi partikel = Nilai eigen dari operator energi.
Menghitung Energi dan Momentum Partikel
Determinan matriks juga dapat digunakan untuk menghitung momentum partikel. Dalam mekanika kuantum, momentum partikel diwakili oleh operator momentum, yang juga dapat direpresentasikan sebagai matriks. Determinan dari matriks operator momentum memberikan informasi tentang momentum partikel.
Momentum partikel = Nilai eigen dari operator momentum.
Determinan matriks merupakan alat penting dalam fisika, memungkinkan kita untuk menganalisis dan memahami berbagai aspek fisika, mulai dari perilaku partikel pada tingkat atom hingga interaksi antara partikel fundamental.
Penutup
Dengan memahami cara menghitung determinan matriks, Anda membuka pintu menuju pemahaman yang lebih dalam tentang aljabar linear. Determinan matriks merupakan alat yang ampuh untuk menyelesaikan berbagai masalah matematika dan ilmiah, mulai dari pemecahan sistem persamaan linear hingga analisis data dalam berbagai disiplin ilmu. Menguasai konsep determinan akan memberikan Anda kemampuan untuk menganalisis dan memecahkan masalah yang lebih kompleks dalam berbagai bidang.
